MARS voting
Introducing a highly accurate single-winner voting method
In a previous post, I explained 4 levels of voting methods ranging from simple to complex, with increasing accuracy. I’ll assume you've read that post, since the method presented here builds on BTR-score, which is introduced in said post. Here, I will introduce a fifth method called "MARS voting". MARS is more accurate than BTR-score but requires an additional step, making it a bit more complicated.
We started with approval voting, then moved through score voting, STAR, and BTR-score. In doing so, we learned about pairwise preferences and extended them to compare all candidates. These are actually two different classes of voting methods. Score voting is a classical cardinal method, focusing solely on the absolute support for each candidate, independent of others. Most Condorcet methods are purely ordinal, considering only the relative preference between pairs of candidates. Philosophical debates among voting scientists discuss which approach is better. STAR and BTR-score attempt to synthesize these two, aiming for practicality over theoretical perfection.
Motivation
There are valid arguments for and against each approach. It's possible to contrive absurd examples to show that either cardinal or Condorcet methods will sometimes select the intuitively "wrong" winner.
Consider the following two candidates, A and B. Each row represents a group of voters with the same preferences. For example, 101 voters rate A as a perfect 100 out of 100, while they rate B almost as high at 99.
| Voters | A | B |
|--------|-----|-----|
| 101 | 100 | 99 |
| 100 | 0 | 99 |In this case, B scores nearly twice as many points as A (19,899 to 10,100), but a majority vote (STAR, BTR-score) would elect A (101 to 100 voters).
Another example:
| Voters | A | B |
|--------|-----|-----|
| 99 | 1 | 0 |
| 1 | 0 | 100 |Here, 99% of voters prefer A over B, but score voting would elect B.
Procedure
Extreme scenarios like these may never occur in real life, but they illustrate that neither philosophy is perfect. What if we could invent a method that selects the "right" system depending on the situation? One that mixes absolute and relative scores?
This is the goal of "Mixed Absolute Relative Score" voting (MARS voting for short). MARS is very similar to BTR-score and still uses the same ballot as score voting. The main difference is that we compare each pair of candidates not only by the number of votes but also by their absolute score.
Voters rate each candidate on a scale from 0 to 5, with blanks counted as 0. Order the candidates from highest to lowest (average) score. Compare the lowest two candidates and drop the loser until only one winner remains. To compare candidates, add the percentage of votes that prefer one over the other, plus the score as a percentage of the maximum possible. The higher combined votes + score wins the match.
Example
Let's look at an example with three candidates, 100 voters, and scores from 0 to 5 (for a maximum possible score of 500). There are three groups of voters who submitted identical ballots.
| Voters | A | B | C |
|--------|-----------|-----------|-----------|
| 32 | 4 | 0 | 5 |
| 33 | 4 | 5 | 5 |
| 35 | 4 | 4 | 0 |
| score | 400 (80%) | 305 (61%) | 325 (65%) |From the total score in the last row, we see that score voting would elect A. Counting pairwise preferences, we find that Condorcet methods elect B. A would lose to both other candidates in a runoff, while B is the score voting loser. Both A and B are simultaneously the "best" and "worst" candidate by some metric.
Now, let's apply MARS voting.
First, order the candidates by total score:
A
C
B
Then, compare them from the bottom up.
In the runoff between B and C, B is preferred by 35% and has a score of 61%, resulting in 35 + 61 = 96 points. C is preferred by 32% and has a score of 65%, resulting in 32 + 65 = 97 points. C wins by 1 point, and B is eliminated. C advances to the match against A.
In the runoff between C and A, C has 65 + 65 = 130 points, while A has 35 + 80 = 115 points. So, A is eliminated, and C is declared the winner.
This also is a unrealistic example. Most of the time, the Condorcet and score voting winners will be the same, and in most other cases, MARS will elect either of them. But even here, there is a case to be made for electing C. When we eliminate the "obviously bad" candidates—the Condorcet loser and the score voting loser—C is left as the least bad choice.
For more examples, see the article on Electowiki.
Accuracy
One argument for using MARS is that it seems to perform well in terms of Voter Satisfaction Efficiency (VSE). How well? If these results hold up, then it's the best voting method by VSE so far. Its performance is in the 99% range for both honest and strategic cases. Compare that to plurality voting, which ranges from about 74% (honest) to 86% (strategic), or ranked pairs, which scores 92% (strategic) to 99% (honest).
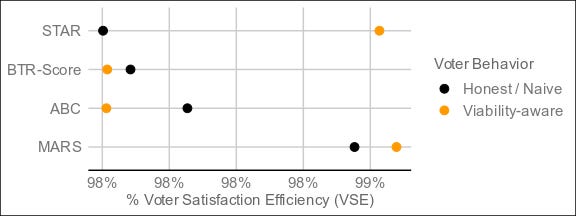
However, VSE isn't a definitive measure. It's the best we have, but we shouldn't place too much confidence in those numbers. The simulations rely on various assumptions, and comparing various simulations reveals some variance in results. The core results, however, are consistent (e.g. Condorcet and score are better than approval, which is better than IRV, which is better than plurality).
The important question is whether the voting method encourages cooperation or competition. As Marcus Ogren argues:
Two takeaways: First, adopting better voting methods matters a lot. Second, far more of the benefits of better voting methods come from reducing political polarization than from having better/more representative leaders; by my calculations, the latter is literally hundreds of times more important.
Does MARS voting achieve that? Certainly, yes. I think any method that allows voters to rate or rank candidates equally and is robust against clones and spoilers would passes this test. As a counterexample, IRV only allows one candidate per rank, which inevitably separates the electorate into non-overlapping groups. Approval, score voting, STAR, and most Condorcet methods impose no such restrictions. Going further, we could take a look at strategic incentives. This however would go beyond the scope of this post.
Use Cases
You might wonder: if the results will be the same as Condorcet and score voting most of the time, why does it matter who wins in rare edge cases? In most situations, simpler methods are sufficient. That's why I didn't include MARS in the previous post on 4 levels of voting methods. However, covering these edge cases also reduces the impact of and incentive for strategic voting, making the system more robust overall.
MARS becomes useful when the electorate has enough knowledge about voting methods (or can be expected to acquire it) so that the transition to MARS requires only little education. I also recommend it in cases where the stakes are so high that the additional complexity is justified. This might include a parliament electing a prime minister or president, or elections in a technically-minded organization (e.g., the Mars Society). In cases where voters don't need to understand the voting method (e.g., an online poll), there’s practically no cost in using MARS.
Conclusion
When I first developed MARS, I was reluctant to recommend it at all. It seemed too complicated with uncertain benefits. Over time, however, I managed to simplify it. Together with the four other methods discussed previously, the learning curve is now more manageable. With the promising preliminary VSE results, I'm now convinced that it, at least, deserves a test in the real world.
Update
A simpler, and likely more robust, version of this idea is to use approvals instead of scores—MARA instead of MARS.
As Marcus Ogren points out on Reddit, there is a risk that MARS would incentivize a min-max strategy in the case of only two viable candidates:
My biggest concern with MARS aside from the complexity, is that, in races with exactly two viable candidates, it strongly incentivizes voters to give one of them a 5 and the other a 0. This could make voting strategically more important under MARS than under STAR (let alone Condorcet). I think strategic voting is the most important research direction for studying MARS.
A potential fix is to count the higher ranges as approvals and the lower ranges as rejections. I'm unsure which way of splitting it would work best, so I'll present two versions: one where only the top-rated candidates count as approved, and one where ratings from 3 to 5 count as approved.
MARA-Top:
Voters rate each candidate on a scale from 0 to 5. Blanks are counted as 0.
Top ratings (5) are counted as approvals.
Order the candidates from highest to lowest sum of approvals.
Compare the lowest two candidates and drop the loser until only one winner remains.
To compare candidates, add the votes that prefer one over the other, plus the approvals for each. The candidate with the higher combined votes and approvals wins the match.
MARA-3-5:
Voters rate each candidate on a scale from 0 to 5. Blanks are counted as 0.
Ratings from 0-2 are rejections; 3-5 are approvals.
Order the candidates from highest to lowest sum of approvals.
Compare the lowest two candidates and drop the loser until only one winner remains.
To compare candidates, add the votes that prefer one over the other, plus the approvals for each. The candidate with the higher combined votes and approvals wins the match.
I'm just throwing out some ideas here. More research is needed.


Is it possible to find an example where the the score winner and Condorcet winners are different, and voters all use the full range of scores? Seems unlikely that people would give A a score of 5, B a score of 4, and C a score of 4, since it's bad strategy to use so little of the full range of expression.